들어가기전
- 이 글의 풀이 방식은 누적합과 구간합을 이용한 방식입니다. 누적합과 구간합을 이미 알고 계신 분들은 쉽게 이해하실 수 있을 겁니다.
- 만약 누적합과 구간합을 모르신다면 공부하고 오시는 걸 추천드립니다. (유튜브 링크)
문제 설명
30461번: 낚시
첫째 줄에 일감호의 크기를 나타내는 정수 $N,M$과 건덕이가 낚싯대를 휘두를 횟수 $Q$가 공백으로 구분되어 주어진다. $\left( 1\leq N,M\leq 2\, 000;\ 1\leq Q\leq 300\, 000 \right)$ 둘째 줄부터 $N$개의 줄에 걸
www.acmicpc.net

문제 이해

- (a, b)에 미끼가 존재할 경우, (1, b) + (2, b) + (3, b) + ... + (a, b) 의 물고기를 사로잡는다.
- 낚시줄을 한 바퀴 감아올리면, 미끼는 (a - 1, b - 1)로 이동하며, 이동한 위치에서 물고기를 사로잡는다.
- 즉, (1, b - 1) + (2, b - 1) + (3, b - 1) + ... + (a - 1, b - 1) 의 물고기를 사로 잡는다.
예시
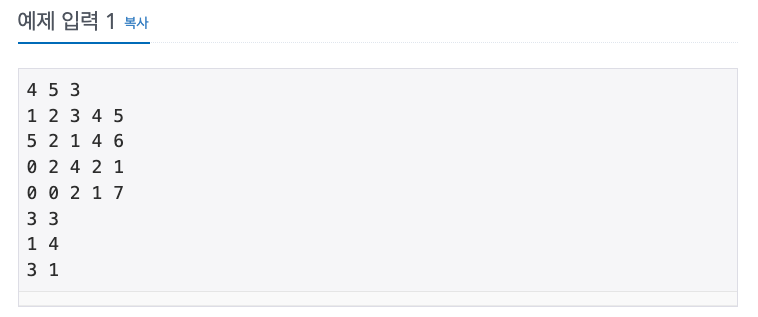
W = 3, P = 3 인 경우,
처음 미끼 위치는 (3, 3) 이므로 (1, 3)부터 (3, 3)까지는 3 1 4
낚시줄을 한 바퀴 감아올리면, (2, 2) 로 이동하므로 (1, 2)부터 (2, 2)까지는 2 2
한 번 더 감아올리면, (1, 1) 로 이동하므로 (1, 1)은 1
한 번 더 감아올리면, 수면 밖으로 나오므로 끝
즉, 잡은 물고기의 합은 3 + 1 + 4 + 2 + 2 + 1 = 13
W = 1, P = 4 인 경우,
처음 미끼 위치는 (1, 4) 인 4
낚시줄을 한 바퀴 감아 올리면, 수면 밖으로 나오므로 끝
즉, 잡은 물고기의 합은 4
W = 3, P = 1 인 경우,
처음 미끼 위치는 (3, 1) 이므로, (1, 1)부터 (3, 1)까지는 1 5
낚시줄을 한 바퀴 감아 올리면, 수면 밖으로 나오므로 끝
즉, 잡은 물고기의 합은 1 + 5 = 6
시간 복잡도 (최악의 경우)
1. 물고기의 수를 입력 받고 하나씩 직접 더하기 (실패)
처음 미끼의 위치인 W 만큼 더하는 횟수 2000
낚시줄을 한 바퀴 감아 올렸을 때, 더하는 횟수 1999
...
마지막은 1
즉, 연산횟수는 2000 + 1999 + ... + 1 = (2000 * 2001) / 2 = 2001000
Q가 300000 이므로 600,300,000,000 (6천억 회)
파이썬 기준으로 2000만회에 1초이므로 연산 시간은 30,015초 걸림
2. 물고기의 수를 입력 받을 때, 세로 줄을 미리 구해놓기 (실패)
처음 미끼의 위치인 W 에 미리 값을 구해놨으니 횟수 1
낚시줄을 한 바퀴 감아 올렸을 때, 연산 횟수 1
...
마지막도 1
즉, 연산 횟수는 가로의 길이만큼인 2000만번
Q가 300000 이므로 600000000 (6억 회)
파이썬 기준으로 30초
3. 물고기의 수를 입력 받을 때, 합을 미리 구해놓기 (성공)
3000만 회를 연산했을 때, 매번 시간복잡도는 O(1)이 걸리므로 값을 입력 받았을 때의 시간복잡도만 영향을 끼침
즉, N=2000, M=2000 일 때, 2000 * 2000 = 4000000(400만) 이므로 연산 시간은 0.2초
풀이

위와 왼쪽을 0 으로 채운 이유는 두 가지입니다.
1. (N, M) 의 인덱스를 맞추기
2. 구간합을 구하기 편리하게 만들기

- 풀이의 핵심은 물고기의 수를 입력 받을 때, 구간합을 통해 테이블에 각 위치에 미리 값을 구해놓는 겁니다.
- 이렇게 되면 예제 입력 1을 기준으로 아래와 같이 답을 바로 구할 수 있습니다.
(3, 3) = 13
(1, 4) = 4
(3, 1) = 6
누적합
아래와 같이 삼각형 모양의 합을 구하면 됩니다.

W=3, P=3 의 값을 구해보도록 하겠습니다.
(3, 3) 의 누적합은 4 1 3 0 / 2 2 0 / 1 0 / 0 의 합인 13입니다. 이 값들을 포함하는 누적합은 (2, 2)과 (2, 3)에서 구한 상태입니다.
(2, 3) 에는 1 3 0 / 2 0 / 0 의 합을 미리 구했고,
(2, 2) 에는 2 2 0 / 1 0 / 0 의 합을 미리 구했습니다.
그럼 (2, 3)과 (2, 2)의 합 그리고 W=3, P=3의 위치에 있는 값인 4를 더하면 될 거 같습니다.
하지만 (2, 3)의 누적합인 5와 (2, 2)의 누적합인 6 그리고 (3, 3)의 값인 4 를 더하면 15가 됩니다. 이는 (3, 3)의 누적합인 13보다 2가 많습니다.
그 이유는 (2, 3)의 누적합과 (2, 2)의 누적합에 중복되는 부분이 있기 때문입니다. 각각 값을 살펴보면
(2, 3) 에는 1 3 0 / 2 0 / 0
(2, 2) 에는 2 2 0 / 1 0 / 0
잘 보면 2 0 / 0 이 중복되는 걸 보실 수 있습니다. 이는 (1, 2)의 누적합에 해당하는 값들입니다.
(위 그림을 몇 분간 살펴보면 확실히 보일 겁니다.)
그럼 이제 (1, 2)의 누적합을 빼보겠습니다.
(2, 3)의 누적합 + (2, 2)의 누적합 + (3, 3)의 값 - (1, 2)의 누적합
= 5 + 6 + 4 - 2
= 13
보시는 것과 같이 구하고자 하는 (3, 3) 누적합인 13을 찾을 수 있습니다.
정리
(3, 3)의 누적합을 구하기 위해서는 (3, 3)에 해당하는 값 + (2, 3) 의 누적합 + (2, 2) 의 누적합 - (1, 2) 의 누적합이었습니다.
이를 공식화하면 (W, P) 의 누적합 = (W, P) 의 값 + (W - 1, P) 의 누적합 + (W - 1, P - 1) 의 누적합 - (W - 2, P) 의 누적합이 됩니다.
다른 부분도 마찬가지입니다.
누적합의 핵심은 이전에 구한 누적합을 더한 다음, 중복되는 부분을 빼는 것이 핵심입니다.
참고
글을 쓰기 위해 그렸던 표를 공유하겠습니다.
https://drive.google.com/file/d/1nq-io4mCEjAQsBdggBUH1olQ9zjybjlj/view?usp=drive_link
백준 30461 낚시.drawio
drive.google.com
'알고리즘 > 백준' 카테고리의 다른 글
| 99클럽 코테 스터디 2일차 TIL (11561번: 징검다리) (0) | 2024.10.29 |
|---|---|
| 99클럽 코테 스터디 1일차 TIL (1072번: 게임) (0) | 2024.10.28 |
| 3009번: 네 번째 점 (c언어) (1) | 2021.03.12 |
| 1929번: 소수 구하기 (c언어) (0) | 2021.02.15 |
| 1989번: 소수찾기 (0) | 2021.02.14 |



댓글